Процедура проверки числа. является ли число числом
теория
Самовлюблённое число, или совершенный цифровой инвариант (англ. pluperfect digital invariant, PPDI) или число Армстронга — натуральное число, которое в данной системе счисления
равно сумме своих цифр, возведённых в степень, равную количеству его
цифр. Иногда чтобы считать число таковым, достаточно, чтобы степени, в
которые возводятся цифры, были равны m — тогда число можно назвать m-самовлюблённым.
Например, десятичное число 153 — число Армстронга, потому что:
- 1³ + 5³ + 3³ = 153
«Есть только четыре числа, исключая единицу, которые равны сумме кубов своих цифр:


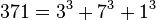
и  . .
практика
{1. Числом Армстронга называется целое n-значное число,
сумма n-х степеней цифр которого равна самому этому числу.
Например, числом Армстронга является число 407,
так как 407 = 4 в 3 степени + 0в 3 степени + 7 в 3 степени.
Найдите все числа Армстронга для заданного n <= 10.
}
// uses math; // для функции power (возведение в степень)
uses crt;
// функция проверки числа Армстронга;
Function GetShisloAmstrong(Value:integer):boolean;
var a1,x,y:integer;
m:array [1..10] of byte;
sum:integer;
begin
a1:=value;
y:=1;
sum:=0;
while (a1 div 10) <> 0 do begin
m[y]:=a1 mod 10; // массив чисел
a1:=a1 div 10;
Y:=y+1;
end;
m[y]:=a1 mod 10;
// определяем кол-во числе в числе
for X:=1 to y do
sum:=sum+round(power(m[x],y));
GetShisloAmstrong:=sum=value;
end;
var n,x:integer;
first:boolean;
Begin
Clrscr;
for n:=1 to 10 do begin first:=true;
for X:=round(power(10,n-1)) to round(power(10,n)) do begin
if GetShisloAmstrong(x) then begin
if first then writeln('Для N = ',n);
first:=false;
writeln(x);
end;
end;
end;
end.
ответ
Для N = 1
1
2
3
4
5
6
7
8
9
Для N = 3
153
370
371
407
Для N = 4
1634
8208
9474
Для N = 5
54748
92727
93084
Для N = 6
548834
Для N = 7
1741725
4210818
9800817
9926315
Для N = 8
24678050
24678051
|



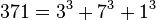
 .
.